■ Hello School 算数 体積・表面積　練習問題　解答と解説　■

インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。

※特に指定がない場合、円周率は3.14とします。

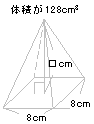
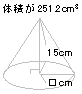
１． アの体積は128cm3、イの体積は251.2cm3です。 それぞれの立体の□の値を求めなさい。 ア イ 解説： ア… 8×8×□× 1 3 ＝128cm3。 □＝6cm。 イ… □×□×3.14×15× 1 3 ＝251.2cm3。 □×□＝16 □＝4cm。 解答：ア＝6cm　イ＝4cm

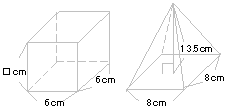
２． 右の図の直方体と四角すいの体積は等しくなって います。□の値を求めなさい。 解説： 四角すいの体積は 8×8×13.5× 1 3 ＝288cm3。 直方体の体積にあてはめると、6×6×□＝288cm3。 □＝8cm。 解答：8cm

３． 右の図の体積を求めなさい。 解説： 底面の三角形は直角二等辺三角形で、別な見方をすればひし形の半分 になっている。 底面の面積は8×8÷2÷2＝16cm2。 求める体積は16×12＝192cm3。 解答：192cm3

４． 右の図のそれぞれの 立体の体積と表面積を 求めなさい。 (1) (2) (3) 解説： (1) 体積…… 10×10×10-5×5×5＝875cm3。 表面積… 10×10×6＝600cm2。 (2) 体積…… 10×10×3.14× 3 4 ×10＋ 10×10×3.14×10＝5495cm3。 表面積… 10×10×3.14×2＋20×3.14× 3 4 ×10 ＋20×3.14×10＋10×10×2＝1927cm2。 (3) 体積…… 10×10×3.14×12＋20×20×3.14×10＝16328cm3。 表面積… 10×10×3.14＋20×20×3.14＋ 20×3.14×12＋40×3.14×10＝3579.6cm2。 解答：(1)体積…875cm3　表面積…600cm2　(2)体積…5495cm3　表面積…1927cm2 　(3)体積…16328cm3　表面積…3579.6cm2

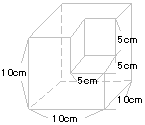
５． 右の(1)は直方体に円柱をさしこんだ もので、(2)は立方体に1辺8cmの 正方形を底面とする直方体で反対 側の面までくりぬいたものです。 それぞれの立体の体積と表面積を 求めなさい。 (1) (2) 解説： (1) 体積…… 4×4×3.14×10＋10×10×4＝902.4cm3。 表面積… 8×3.14×10＋10×10×2＋10×4×4＝611.2cm2。 (2) 体積…… くりぬく前の体積は10×10×10＝1000cm3。 1回目にくりぬく体積は8×8×10＝640cm3。 2回目と3回目にくりぬく体積は640-8×8×8＝128cm3ずつ。 求める体積は1000-640-128×2＝104cm3。 表面積… （10×10-8×8）×6＋（1×8×4）×6＝408cm2。 解答：(1)体積…902.4cm3　表面積…611.2cm2 　(2)体積…104cm3　表面積…408cm2

６． 右の図のように、直方体の１つの面に底面が正方形の四角柱 をくりぬいたところ、体積が144cm3減って、表面積が96cm2 増えました。 くりぬいた深さは何cmですか。 解説： 表面積が増えた部分は四角柱の側面積の部分である。 96÷4＝24cm2。（側面積の1つ分） 24×四角柱の正方形の1辺（高さ）＝144cm3。 正方形の1辺＝6cm 6×6×くりぬいた深さ＝144cm3。 くりぬいた深さは4cm。 解答：4cm

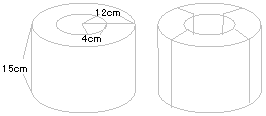
７． 右の図のような円柱を4等分しました。 1つ分の表面積を求めなさい。 解説： （12×12×3.14-4×4×3.14）×2 　＋8×3.14×15＋24×3.14×15＝2311.04cm2。 2311.04÷4＝577.76cm2。 577.76＋8×15×2＝817.76cm2。 解答：817.76cm2

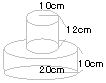
８． 右の図は半径4cm、高さ16cmの円柱を、円を4等分しながら4cmずつ階段状 にした立体です。 立体の体積と表面積を求めなさい。 解説： 体積…… 4×4×3.14×4×（1+ 3 4 + 1 2 + 1 4 ）＝50.24cm3。 表面積… 8×3.14×4×（1+ 3 4 + 1 2 + 1 4 ） 側面積 ＋4×4×6 ＋ 4×4×3.14×2 1辺が4cmの 正方形の数 底面積2つ分 ＝447.68cm2。 解答：体積…50.24cm3　表面積…447.68cm2

９． 右の図のような立方体に円すいをくりぬきました。この立体の 体積を求めなさい。 解説： 30×30×30-15×15×3.14×30× 1 3 ＝19935cm3。 解答：19935cm3

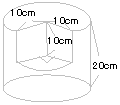
10． 右の図のような底面が台形で高さが10cmの四角柱から 半径12cm高さ10cmの円柱の半分をくりぬきました。 立体の体積と表面積を求めなさい。 解説： 体積…… ｛（4+28）×24÷2-12×12×3.14÷2｝×10＝1579.2cm3。 表面積… ｛（4+28）×24÷2-12×12×3.14÷2｝×2 　＋24×3.14÷2×10＋4×10＋10×24＋10×28 　＋8×10＝1332.64cm2。 解答：体積…1579.2cm3　表面積…1332.64cm2

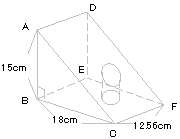
11． 右の図のように三角柱に半径3cmの穴をあけたところ、 体積が5％減りました。 穴の中心は面ABEDから何cm離れていますか。 解説： 穴の体積は15×18÷2×12.56×0.05 ＝84.78cm3。 中心の高さは84.78÷（3×3×3.14）＝3cm。 右の図で三角形ABCと三角形PQCは相似 なので、BQの長さは14.4cm。 解答：14.4cm

12． 右の図の円すいを半分した立体があります。 立体の体積と表面積を求めなさい。 解説： 体積…… 9×9×12×3.14× 1 3 × 1 2 ＝226.08cm3。 表面積… 18×12÷2＋9×9×3.14× 1 2 ＋15×15×3.14× 3 5 × 1 2 ＝447.12cm2。 解答：(1)226.08cm3　(2)447.12cm2

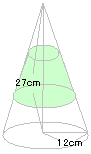
13． 右の図のような円すいを高さを3等分するように分けました。 真ん中の黄緑の部分の体積を求めなさい。 解説： 1番上の円すい、2段目のえんすい台、3段目の円すい台の体積の 比は1：7：19。求める体積は 12×12×3.14×27× 1 3 × 7 27 ＝1055.04cm3。 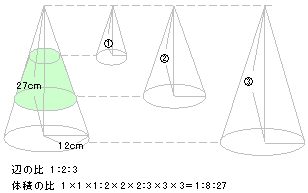解答：1055.04cm3

14． 右の図のような円すいを高さが半分になるところで 切り取り、さかさにしてもとの円すいにさしこみました。 黄緑の部分の体積を求めなさい。 解説： 切り取った円すいの体積と円すい台の体積の比は1：7。求める体積は 12×12×3.14×8× 1 3 × 7 8 ＝1055.04cm3。 解答：1055.04cm3

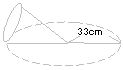
15． 右の図のように、体積が4521.6cm3の円すいを横にしてすべら ないように転がしたところ、半径33cmの点線の円周上を2回転と 3 4 回転して1周しました。円すいの高さを求めなさい。 解説： 底面の半径×回転数＝母線なので、底面の半径は 底面の半径×2 3 4 ＝33。 底面の半径は12cm。 12×12×3.14×高さ× 1 3 ＝4521.6。 高さは30cm。 解答：30cm

16． 右の図のように、1辺が15cmの正方形を 5枚横に並べました。 台形ABEDをABを軸として1回転させて できる立体の体積と台形ECFGをECを軸 として1回転させてできる立体の体積の 差を求めなさい。 解説： （ア＋イ）−（イ＋ウ） ＝ア−ウになるので、 正方形ABCDを1回転 させた体積から三角形 BFGを引いた体積を 求めればよい。 三角形の相似から、FGは6cmになるので、 10×10×3.14×10＝3140cm3。 20×20×3.14×6−20×20×3.14×6× 1 3 ＝5024cm3。 5024-3140＝1884cm3。 解答：1884cm3

体積・表面積の解説ページ　　　練習問題

算数目次　　算数・数学のページ Top この授業を担当する大川葵先生です

商用目的での利用を固く禁じます。