■ Hello School 算数 図形の移動　練習問題　解答と解説　■

インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。

※特に指定がない場合、円周率は3.14で計算します。

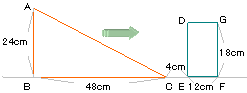
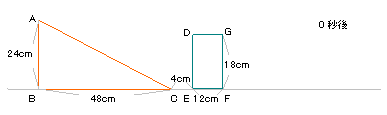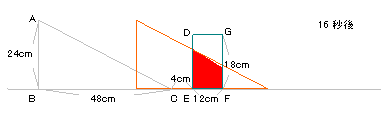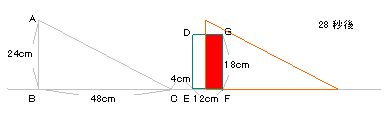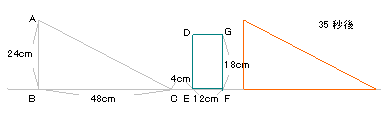
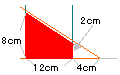
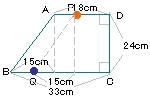
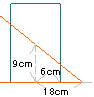
１． 右の図のように、直角三角形が毎秒2cmの速さで 矢印の方向に進み、長方形と重なって移動して いきます。 (1)10秒後に2つの図形が重なった部分の面積は 　何cm2ですか。 (2)長方形DEFGの面積が直角三角形によって 　二等分されるのは何秒後ですか。 解説： (1) 10秒後の図形の重なりは右の図の通り。 また、直角三角形の垂直の部分の辺の比は2：1に なる。 求める面積は （8+2）×12÷2＝60cm2。 (2) 長方形の面積を直線で二等分するのは、下の図 のように対角線の交点を通る場合である。 そのときの直角三角形と長方形の位置は右の図 ようなときであり、CがFよりも12cm進んだところに なるので、Cが28cm移動したときである。 求める時間は28÷2＝14秒後。 解答：(1)60cm2　(2)14秒後

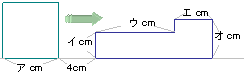
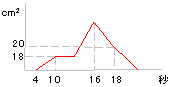
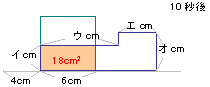
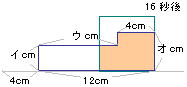
２． 右の図のように、正方形が矢印の方向に 長方形を組み合わせた図形に重なりながら 毎秒1cmの速さで移動していきます。 グラフは2つの図形が重なったときの面積を 表したものです。 (1)ア〜オの長さをそれぞれ求めなさい。 (2)重なった部分の面積が2回目に23cm2に 　なるのは正方形が動き始めてから何秒後 　ですか。 解説： (1) 10秒後の図形の位置は右上の状態と なり、アは6cm、イは18÷6＝3cmという ことがわかる。 右下の18秒後から、エは4cm、オは 20÷4＝5cm、ウは14-6＝8cmとなる。 (2) 2回目に23cm2になるのはグラフから16 秒後から18秒後の間で、16秒後には右 の図のように面積は26cm2になる。 1秒ごとに3cm2ずつ減るので、面積が 23cm2になるのは17秒後。 解答：(1)ア…6cm　イ…3cm　ウ…8cm　エ…4cm　オ…5cm　(2)17秒後

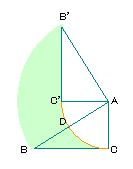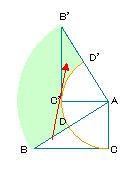
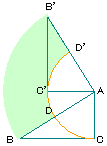
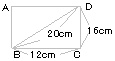
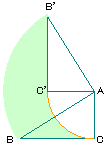
３． 右の図はAB＝10cm、BC＝8cm、AC＝6cmの直角三角形ABCをAを 中心に90°回転させたものです。黄緑の部分の面積は何cm2ですか。 解説： 下の図のようにBDCの部分をB'D'C'に移動させると、中心角90°で半径10cm のおうぎ形の面積から中心角90°で半径6cmのおうぎ形の面積を引けば 答えが求まる。 10×10×3.14× 1 4 − 6×6×3.14× 1 4 ＝16×3.14＝50.24cm2。 → → 解答：50.24cm2

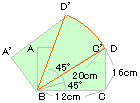
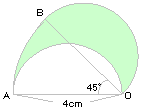
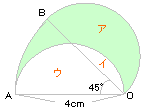
４． 右の図は直径4cmの半円を45°回転させたものです。 黄緑の部分の面積は何cm2ですか。 解説： 右の図でア＋イ＝イ＋ウとなるので、 ア＝ウ。 求める面積は半径4cm、中心角45°の おうぎ形の面積を求めればよい。 4×4×3.14× 1 8 ＝6.28cm2。 解答：6.28cm2

５． 右の図は長方形ABCDをBを中心に45°回転させたものです。 黄緑の部分の面積は何cm2ですか。 解説： 下の図のように、求める面積は全体から長方形の面積を引けばよい。 16×12÷2×2＋20×20×3.14× 1 8 −16×12＝157cm2。 − ＝ 解答：157cm2

６． 右の図は、AB＝8cm、BC＝6cm、対角線AC＝10cmの 長方形をもとの位置までころがしたものです。 (1)Aが動いた長さは何cmですか。 (2)黄緑の部分の面積は何cm2ですか。 解説： (1) 20×3.14× 1 4 ＋12×3.14× 1 4 ＋16×3.14× 1 4 ＝ 12×3.14 ＝37.68cm。 (2) 半径10cm、中心角90°のおうぎ形から長方形の面積を引けばよい。 10×10×3.14× 1 4 −6×8＝30.5cm2。 解答：(1)37.68cm　(2)30.5cm2

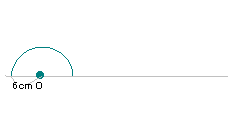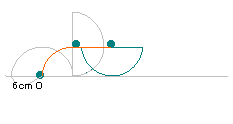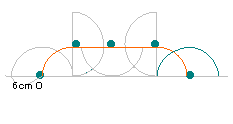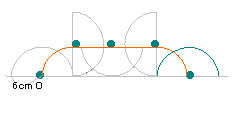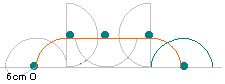
７． 右の図は半径6cmの半円をすべることなく一回転 させたものです。中心Oが動いた長さは何cmですか。 解説： 中心Oが動く軌跡は上の図のようになる。 求める長さは 12×3.14× 1 4 ×2＋12×3.14× 1 2 ＝12×3.14＝37.68cm。 解答：37.68cm

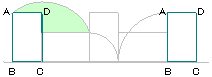
８． 右の図は長方形ABCDとABを直径とする 半円を組み合わせた図形をすべることなく 一回転させたものです。 AB＝ED＝8cmであるとき、Eが動いた長さ は何cmですか。 解説： Eが動く軌跡は右の図の ようになる。求める長さは 16×3.14× 1 4 ＋8×3.14× 1 2 ＋16×3.14× 1 4 ＝12×3.14＝37.68cm。 解答：37.68cm

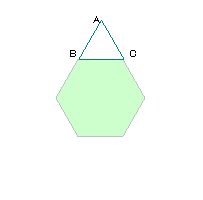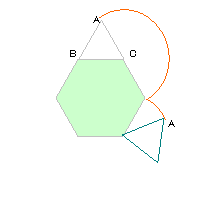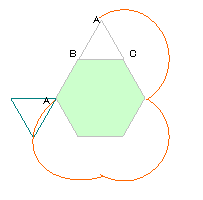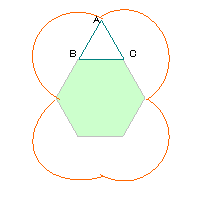
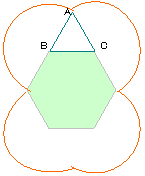
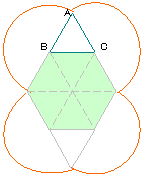
９． 右の図のような1辺6cm、面積が93.42cm2の正六角形があり、周りを1辺 6cmの正三角形をすべることなく元の位置にもどるまで回転させます。 (1)Aが動いた長さは何cmですか。 (2)(1)のときのAの動いたあとの線と正六角形に囲まれる図形の面積は 　何cm2ですか。 解説： (1) Aが動く軌跡は 右の図の通り。 半径6cmの半円が 4個分、または円が 2個分になるので、 12×3.14×2 ＝75.36cm。 (2) 求める面積は円が 2個と正三角形2個 になる。 正六角形は正三角 形を6個あわせた ものなので、1個分 の面積は 93.42÷6＝15.57。 求める面積は 6×6×3.14×2 ＋15.57×2 ＝257.22cm2。 解答：(1)75.36cm　(2)257.22cm2

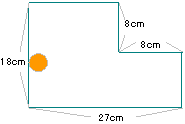
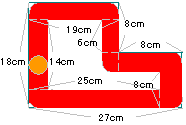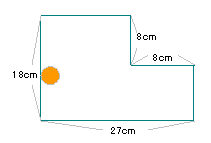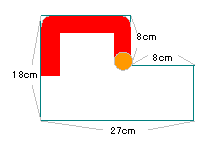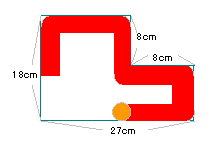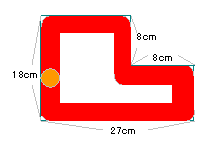
10． 右の図のような直方体を組み合わせた図形の内側を 半径1cmの円が辺にそって1周します。 円が通ったあとの面積は何cm2ですか。 解説： 円が通る軌跡は上のようになる。 （2×2-1×1×3.14）×5＝4.3…角を曲がるときの通らない部分 求める面積は 19×2＋6×2＋8×2＋8×2＋25×2＋14×2 ＋2×2×3.14× 1 4 −4.3＝168.26cm2。 解答：168.26cm2

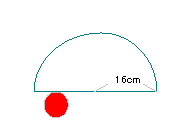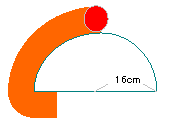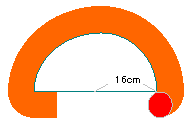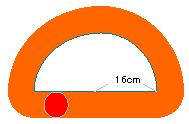
11． 右の図のような半径16cmの半円の外側を半径4cmの円が 1周します。円が通ったあとの面積は何cm2ですか。 解説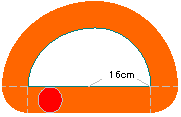： 円が通る軌跡は上のようになる。求める面積は 8×32＋8×8×3.14× 1 4 ×2＋24×24×3.14× 1 2 -16×16×3.14× 1 2 ＝808.64cm2。 解答：808.64cm2

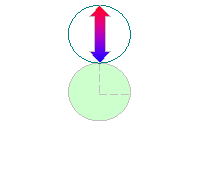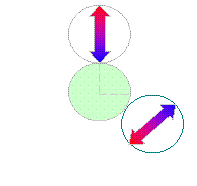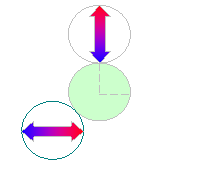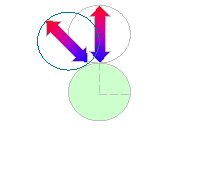
12． 右の図のように、 黄緑の円の周りを 同じ半径の矢印の ついた円を1周させ ました。 (1)円がAの位置に 　きたとき、矢印は 　ア〜クのどの方向 　を向いていますか。 (2)円が1周したとき、 　何か移転しますか。 ア イ ウ エ オ カ キ ク 解説： (1) 下の図のように赤い部分が重なり合う のでオ。 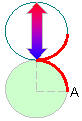(2) 右の図のように2回転。 解答：(1)オ　(2)2回転

13． 右の図のように、黄緑の円の周りを同じ半径の赤い円 を1周させました。赤い円は何回転しますか。 解説： 同じ半径の円が1周すると、2回転 する。 赤い円の中心が動く軌跡は右の図 である。中心は 1 2 ×2＋ 1 3 ×2＋ 1 6 ＝1 5 6 回転するので、赤い円は 1 5 6 ×2＝3 2 3 回転する。 解答：3 2 3 回転

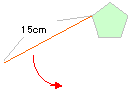
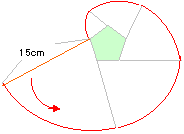
14． 右の図のような1辺が3cmの正五角形の頂点に15cmのひもを つけ、矢印の方向にまきつけていきました。 ひもが動ける面積を求めなさい。 解説： ひもが動く軌跡は右の図のようになる。 求める面積は 15×15×3.14× 1 5 +12×12×3.14× 1 5 ＋9×9×3.14× 1 5 ＋6×6×3.14× 1 5 ＋3×3×3.14× 1 5 ＝495×3.14× 1 5 ＝99×3.14＝310.86cm2。 解答：310.86cm2

15． 右の図のような長方形の点AからPが毎秒1cmの速さで D→C→Bの順序で進みます。三角形ABPの面積が 30cm2になるのは何秒後ですか。 解説： ABを底辺としたとき、面積が 30cm2になるのはAPが6cm、BPが6cm のときなので6秒後と46秒後。 解答：6秒後と46秒後

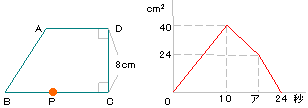
16． 右の図のような台形の辺の上をPが 毎秒1cmの速さでBを出発してC→D →Aの順で進んでいきます。 このときの三角形PABの面積が右の グラフで表されています。 (1)アはいくつですか。 (2)台形ABCDの面積は何cm2ですか。 解説： (1) PがCにきたときの面積が40cm2なので、BCの長さは10cmということが わかる。 グラフからPがアにくるのはDにきたときなので、アは18秒後。 (2) 24秒後で面積が0cm2になることからADは6cm。 台形ABCDの面積は（6+10）×8÷2＝64cm2。 解答：(1)18　(2)64cm2

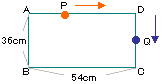
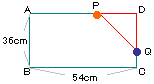
17． 右の図のような長方形があり、PはAから毎秒4cmの速さで、 QはDから毎秒5cmの速さで矢印の方向に長方形の辺上を まわっていきます。 (1)QがPに追いつくのは何秒後ですか。 (2)三角形DPQがはじめて直角二等辺三角形になるのは 　何秒後ですか。 解説： (1) 2つの点が最初にはなれているのは126cmなので、QがPに追いつくのは 126÷（5-4）＝126秒後。 (2) 直角二等辺三角形になるのは、右の図のように PD＝DQとなるので、PとQが進んだきょりの和が 54cmになるときである。 54÷（4+5）＝6秒後。 解答：(1)126秒後　(2)6秒後

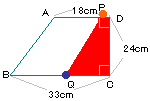
18． 右の図のような台形があり、PはCを出発して毎秒4cmの速さで D→Aの順で進み、QはCを出発して毎秒3cmの速さでBに進み ます。 (1)7秒後の四角形PQCDの面積は何cm2ですか。 (2)四角形PQCDの面積が384cm2になるのは何秒後ですか。 (3)四角形ABQPが平行四辺形になるのは何秒後ですか。 解説： (1) 7秒後のPはAD上のDから4cmのところにあり、 QはCから21cmのところにあるので、面積は （4+21）×24÷2＝300cm2。 (2) 6秒後のときの三角形P(D)QCの面積は216cm2。 その後は1秒ごとに（3+4）×24÷2＝84cm2ずつふえていくので、 （384-216）÷84＝2秒後。 四角形PQCDの面積が384cm2になるのは、8秒後となる。 (3) PがDにつくのが6秒後でこのときのQはCから 18cmすすんだところにある。 四角形ABQPが平行四辺形になるのはPQが 15cmになるときなので、3cmきょりをちぢめれ ばよい。 3÷（4-3）＝3秒後で、出発してから9秒後となる。 解答：(1)300cm2　(2)8秒後　(3)9秒後

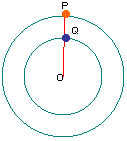
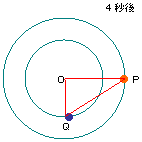
19． Oを中心とする半径4cmの円と半径6cmの円があり、Pは半径8cmの 円を1周するのに16秒、Qは半径4cmの円を1周するのに8秒かかり ます。P、Q、Oが一直線にあるとこからスタートさせ、16秒後までを 考えます。 三角形OPQの面積が最も大きくなるのは何秒後ですか。また、 そのときの面積は何cm2ですか。 解説： Pは1周するのに16秒かかること から1秒で22.5°、Qは1周に8秒 かかることから1秒で45°動くこと になり、1秒で22.5°の差がつく。 面積が最も大きくなるのはOPと OQのつくる角度が90°になるとき で、 90÷22.5＝4秒後と、 270÷22.5＝12秒後となる。 そのときの面積は 4×6÷2＝12cm2。 解答：4秒後と12秒後　12cm2

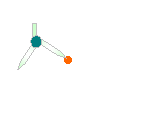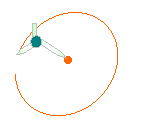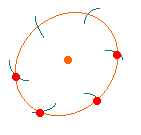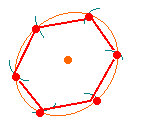
20． 右の赤い点を中心とする半径8cmの円をかき、その周上にすべての頂点が 通るような正六角形を作図しなさい。 解説： 右の図のように半径8cmの円をかき、 コンパスを8cmの状態にして円周を6等分し、 直線で結ぶ。 解答：解説参照

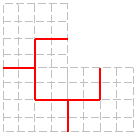
21． 右の図のような図形を4つの合同の図形に分けなさい。 解説： 右の図のように48cm2を4等分するので、 12cm2ずつに分ければよい。 解答：解説参照

図形の移動の解説ページ　　　練習問題

算数目次　　算数・数学のページ Top この授業を担当する大川葵先生です

商用目的での利用を固く禁じます。