| (4) |
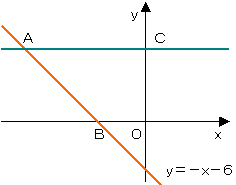
Aのx座標を-tとすると、
y座標はt-6でこれが
台形の高さに当たる。
AC=t、BO=6になるので、 |
|
|
これを解いて、t=±12
Aのx座標は-12になる。 | |
 |
|
|
| (6) |
定価は2000(1+0.1a)=2000+200a
売値は(2000+200a)(1+0.1a)=3920 |
|
|
| (7) |
問題の経過を表に整理すると以下のようになる。
| |
はじめ |
→ |
agの食塩水を
取り出す |
→ |
agの水を
入れる |
→ |
2agの食塩水
を取り出す |
→ |
3agの水を
入れる |
| 食塩水 |
200 |
|
200-a |
|
200 |
|
200-2a |
|
200-2a+3a |
| 濃度 |
0.16 |
|
0.16 |
|
0.16(200-a)
200 |
|
0.16(200-a)
200 |
|
0.064 |
| 食塩水 |
32 |
|
0.16(200-a) |
|
0.16(200-a) |
|
0.16(200-a)(200-2a)
200 |
|
0.16(200-a)(200-2a)
200 | |
|
| 0.064(200-2a+3a)= |
0.16(200-a)(200-2a)
200 |
これを解いて、a=40,300 | |
|
|
| (8) |
出会うまでの時間をx時間後とすると、出会った場所はA地点から8x。
| Bouzu先生の速さは8x÷ |
4
3 |
になり、x時間の距離が30-8xになるので、 |
| (8x÷ |
4
3 |
)x=30-8x |
これを解いて、x=-3, |
5
3 | |
 | |
|
|
| (9) |
① 一段目の花火が開くまでの時間をt秒後とすると、
| 30t-5t2=340( |
70
17 |
-t) |
これを解いて、t=4,70 | |
|
|
|
② ニ段目の花火が開くまでの時間をt秒後とすると、
| 20t-5t2+40=340{ |
88
17 |
-(4+t)} |
これを解いて、t=2,70 | |
|
(10点×10問=100点) |